Depth and Breadth first search (DFS) and (BFS)

Depth-First Search (DFS)

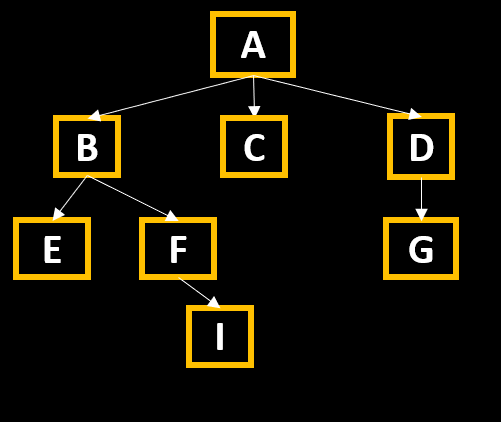
Depth-First Search (DFS) is an algorithm used for traversing or searching tree or graph data structures. It starts at a source node and explores as far as possible along each branch before backtracking. In other words, it goes as deep as possible in one direction before exploring other directions. DFS can be implemented using recursion or by using a stack data structure.

The main steps of the DFS algorithm are as follows:

1. Start at the source node.
2. Explore a neighbor of the current node as deeply as possible.
3. Backtrack if necessary and continue exploring other neighbors.
4. Repeat until all nodes are visited.

DFS is often used in pathfinding, topological sorting and solving problems related to connected components in graphs.

          class Graph:
            def __init__(self):
                # Initialize an empty dictionary to store the graph as an adjacency list
                self.graph = {}
        
            def add_edge(self, u, v):
                # Add an edge to the graph. If the source node is not in the graph, add it with an empty list.
                if u not in self.graph:
                    self.graph[u] = []
                # Add the destination node to the list of neighbors for the source node.
                self.graph[u].append(v)
        
            def dfs(self, start):
                # Set to keep track of visited nodes
                visited = set()
                # Start DFS from the given node
                self._dfs(start, visited)
        
            def _dfs(self, node, visited):
                # If the node is not visited, visit it and mark it as visited
                if node not in visited:
                    print(node, end=' ')
                    visited.add(node)
                    # Get the neighbors of the current node
                    neighbors = self.graph.get(node, [])
                    # Recursively perform DFS on each neighbor
                    for neighbor in neighbors:
                        self._dfs(neighbor, visited)
            
            def toString(self):
                print(self.graph)
                
            # Example usage:
            graph = Graph()
            graph.add_edge(1,2)
            graph.add_edge(1,3)
            graph.add_edge(1,4)
            graph.add_edge(4,3)
            graph.add_edge(4,7)
            graph.add_edge(3,8)
            
            
            
            graph.toString()
            
            print("DFS starting from node 1:")
            graph.dfs(1)
          

Breadth-First Search (BFS)

Breadth-First Search (BFS) is another algorithm used for traversing or searching tree or graph data structures. Unlike DFS, BFS explores all the neighbors of a node before moving on to the next level of nodes. It starts at a source node and explores all nodes at the current depth before moving on to nodes at the next depth. BFS can be implemented using a queue data structure.

The main steps of the BFS algorithm are as follows:

1. Start at the source node and enqueue it.
2. Dequeue a node, visit it and enqueue its neighbors.
3. Repeat step 2 until the queue is empty.

BFS is particularly useful for finding the shortest path between two nodes in an unweighted graph. It is also commonly used in tasks like network broadcasting, social network analysis and solving problems where the solution is close to the source node.

In summary, DFS and BFS are both algorithms for traversing or searching graphs, but they differ in their exploration strategies. DFS explores as deeply as possible along each branch, while BFS explores all the neighbors of a node before moving on to the next level.

            class Graph:
              def __init__(self, name):
                  self.children = []
                  self.name = name
          
              def addChild(self, name):
                  self.children.append(Graph(name))
                  return self
          
              def breadthFirstSearch(self, array):
                  queue = [self]
                  while len(queue) > 0:
                      current = queue.pop(0)
                      array.append(current.name)
                      for child in current.children:
                          queue.append(child)
                  return array
                      
            # Create nodes and build a tree
            root = Graph("A")
            root.addChild("B").addChild("C")
            root.children[0].addChild("D").addChild("E")
            root.children[1].addChild("F").addChild("G")
            
            # Perform breadth-first search
            result = root.breadthFirstSearch([])