15 Best Patterns you have to know as a developer

Coding is about using patterns wisely

Prefix Sum

Two Pointer

Sliding Window

Fast & Slow Pointer

Linked List In-Place Reversal

Monotonic Stack

Top 'k' Elements

Quick Select

Overlapping Intervals

Modified Binary Search

Depth-First Search(DFS)

Breadth-First Search(BFS)

Matrix Traversal

Backtracking

Dynamic Programming

1 - Prefix Sum

It allows for quick calculations of the sum of any subarray (continuous section of the array).

First sum all the items in the array iterating through all of them.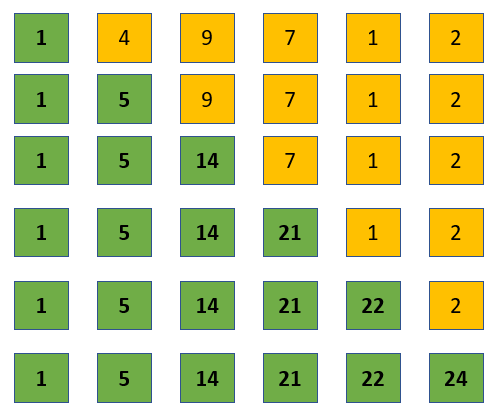

Once you get the sum you can get your answer.

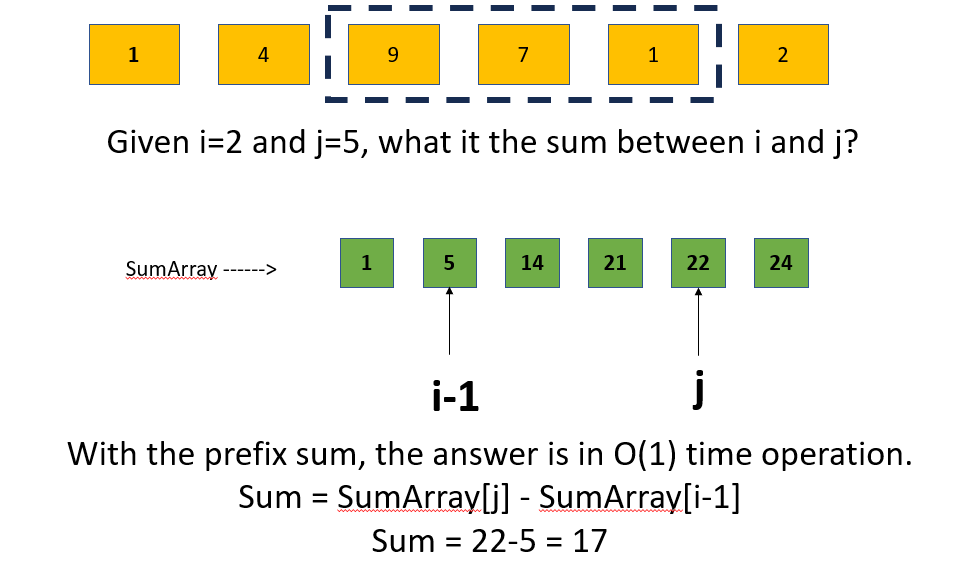
Without a prefix sum, you would need to loop through the subarray to calculate the sum, which takes linear time, O(n). With the prefix sum array, you can do it in constant time O(1). And YES, it will work even with negative number.
Three exercise to practice:

303 - Range Sum Query,

525 - Continuos Array,

560 - Sub Array Sum Equals Array

## Prefix sum
def prefix_sum(arr):
  prefix = [0] * len(arr)
  prefix[0] = arr[0]

  for i in range(1, len(arr)):
      prefix[i] = prefix[i - 1] + arr[i]

  return prefix

arr = [3, 2, 1, 4]
prefix = prefix_sum(arr)
print(prefix)  # Output: [3, 5, 6, 10]

# To get the sum of arr[1...3] (i.e., [2, 1, 4]):
l, r = 1, 3
sum_l_r = prefix[r] - (prefix[l-1] if l > 0 else 0)
print(sum_l_r)  # Output: 7

## Prefix sum
import java.util.Arrays;

public class PrefixSum {
  
  // Function to compute the prefix sum array
  public static int[] computePrefixSum(int[] arr) {
      int n = arr.length;
      int[] prefixSum = new int[n];

      // First element of prefixSum is the same as the original array
      prefixSum[0] = arr[0];

      // Build the prefix sum array
      for (int i = 1; i < n; i++) {
          prefixSum[i] = prefixSum[i - 1] + arr[i];
      }

      return prefixSum;
  }

  public static void main(String[] args) {
      // Example array
      int[] arr = {3, 1, 5, 12, 2, 11};

      // Compute the prefix sum
      int[] prefixSum = computePrefixSum(arr);

      // Print the original array
      System.out.println("Original array: " + Arrays.toString(arr));

      // Print the prefix sum array
      System.out.println("Prefix sum array: " + Arrays.toString(prefixSum));
  }
}

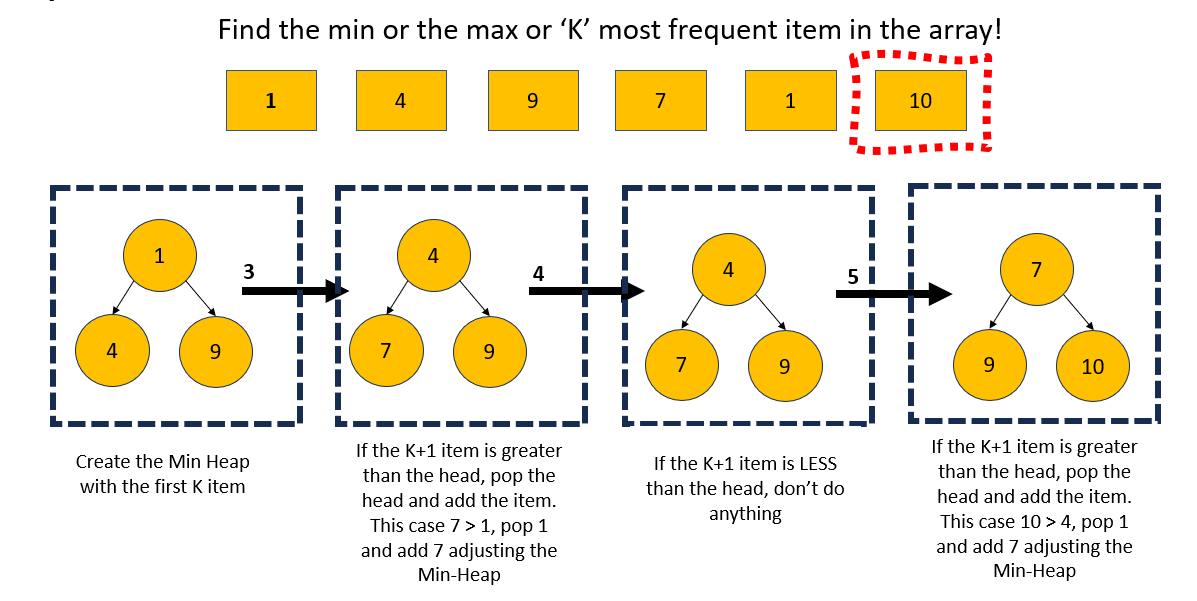
7 - Top 'k' Elements

Finding the top 'k' elements in an array or dataset refers to identifying the 'k' largest or smallest elements from a given collection

Common Approaches to Find Top K Elements

Sorting (Simple but Inefficient, just sort the array O(nlog(n)) and take the first or the last item)
Using a Min-Heap (for Top K Largest)
Using a Max-Heap (for Top K Smallest)
Quickselect Algorithm (Average Time Complexity: O(n))

Using a Min-Heap (for Top K Largest)

Use a min-heap to efficiently find the largest K elements.

A min-heap keeps the smallest element at the root. We maintain a heap of size K. As we iterate over the array, we compare each element with the root of the heap (the smallest element in the heap):

If the current element is larger than the root, replace the root with the current element and heapify.
After iterating through the array, the heap will contain the top K largest elements.

Time Complexity: O(n log k) where n is the size of the array, and k is the size of the heap.

Steps:

Create a min-heap and add the first K elements.
For each element after the first K, if it is larger than the root of the heap, replace the root with the current element and re-heapify.
At the end of the process, the heap will contain the K largest elements.

Using a Max-Heap (for Top K Smallest)

Use a max-heap to efficiently find the smallest K elements.

A max-heap keeps the largest element at the root. We maintain a heap of size K. As we iterate over the array, we compare each element with the root of the heap (the largest element in the heap):

If the current element is smaller than the root, replace the root with the current element and heapify.
After iterating through the array, the heap will contain the top K smallest elements.

Time Complexity: O(n log k) where n is the size of the array, and k is the size of the heap.

Steps:

Create a max-heap and add the first K elements (use negation to simulate a max-heap if needed).
For each element after the first K, if it is smaller than the root of the heap, replace the root with the current element and re-heapify.
At the end of the process, the heap will contain the K smallest elements.

Three exercise to practice:

215. Kth Largest Element in an Array

347. Top K Frequent Elements,

373. Find K Pairs with Smallest Sums

## Top 'K' Largest Item with Min-Heap
import heapq

def find_top_k_elements(arr, k):
    # Step 1: Create a min-heap with first K elements
    min_heap = arr[:k]
    heapq.heapify(min_heap)

    # Step 2: Process the rest of the array
    for num in arr[k:]:
        if num > min_heap[0]:
            heapq.heapreplace(min_heap, num)

    return min_heap

# Example usage
arr = [3, 2, 1, 5, 6, 4]
k = 3
print(find_top_k_elements(arr, k))

## FIND THE K SMALLEST ITEM
def find_k_smallest_elements(arr, k):
    # Step 1: Create a Max-Heap by negating the first K elements
    max_heap = [-num for num in arr[:k]]
    heapq.heapify(max_heap)

    # Step 2: Iterate through the rest of the array
    for num in arr[k:]:
        # If the current element is smaller than the largest in the heap
        if num < -max_heap[0]:
            # Replace the largest (smallest in original) element in the heap
            heapq.heapreplace(max_heap, -num)

    # Step 3: Convert the max heap back to positive numbers
    return [-num for num in max_heap]

# Example usage
arr = [3, 2, 1, 5, 6, 4]
k = 3
print(find_k_smallest_elements(arr, k))

## Top 'K' Largest Item with Min-Heap
import java.util.PriorityQueue;

public class TopKElements {

    public static int[] findTopK(int[] arr, int k) {
        // Step 1: Create a min-heap (PriorityQueue) with the first K elements
        PriorityQueue minHeap = new PriorityQueue<>();

        for (int i = 0; i < k; i++) {
            minHeap.add(arr[i]);
        }

        // Step 2: Process the rest of the array
        for (int i = k; i < arr.length; i++) {
            if (arr[i] > minHeap.peek()) {
                minHeap.poll();  // Remove the smallest element
                minHeap.add(arr[i]);
            }
        }

        // Convert the heap to an array
        int[] result = new int[k];
        for (int i = 0; i < k; i++) {
            result[i] = minHeap.poll();
        }

        return result;
    }

    public static int[] findKSmallestElements(int[] arr, int k) {
      // Step 1: Create a Max-Heap using PriorityQueue with reverse order
      PriorityQueue maxHeap = new PriorityQueue<>(Collections.reverseOrder());

      // Step 2: Add the first K elements to the heap
      for (int i = 0; i < k; i++) {
          maxHeap.add(arr[i]);
      }

      // Step 3: Iterate through the rest of the array
      for (int i = k; i < arr.length; i++) {
          if (arr[i] < maxHeap.peek()) {
              // Replace the largest element in the heap with the current smaller element
              maxHeap.poll();
              maxHeap.add(arr[i]);
          }
      }

      // Step 4: Convert the heap to an array of size K
      int[] result = new int[k];
      for (int i = 0; i < k; i++) {
          result[i] = maxHeap.poll();
      }

      return result;
  }

    public static void main(String[] args) {
        int[] arr = {3, 2, 1, 5, 6, 4};
        int k = 3;
        int[] result = findTopK(arr, k);
        int[] resultSmallest = findKSmallestElements(arr, k);


        for (int num : result) {
            System.out.print(num + " ");
        }
        // Output: 4 5 6

        for (int num : resultSmallest) {
          System.out.print(num + " ");
        }
       // Output: 3 2 1
    }
}